Shaded Area

Finding the shaded area of an object is not that difficult if you are familiar with finding area of compound figures.

See the image below. It is a compound figure with two triangles. 

To find the shaded area, we need to find the area of the BIGGER TRIANGLE and the SMALLER TRIANGLE and find the DIFFERENCE between them.

Area of bigger/outer triangle = 1/2 b x h

                              = 1/2 x 32 x 24

                              = 384m²

 

Area of smaller/inner triangle = 1/2 b x h

                               = 1/2 x 20 x 16

                               = 160m²

 

Area of shaded region = Area of bigger triangle – Area of smaller triangle

                      = 384 - 160

                      = 224m²

Watch the video below on finding the Area of a shaded region: 

Also, try on this quick exercise and see how you do:

https://drive.google.com/file/d/1X7fKr_WVW-oy2x1UJmYd7bgTyYNzoSzb/view?usp=sharing

Perimeter and Area (Compound Figures)

 If you are familiar with finding perimeter and Area of individual shapes, you will just need to learn few things to get a hang of finding perimeter and area of compound figures.

Look at the shape below and ,et's try to find the perimeter and area of this figure.

Upon close inspection we can see that it's two rectangles that are 'stuck' together. 

We don't have to get all worked u for this small question. 

For perimeter, we can simply add all the sides, since perimeter is the boundary outside the figure.

So total perimeter of this figure would be:

Perimeter = 7 + 11 + 2 + 7 + 5 +4

          = 36 cm

(Remember to find the length of any missing sides before adding).

Now for area, we can use the formula of a rectangle and find individual areas of the two rectangles inside the figure and add them up. (Area is the total space taken up by the figure). 

                

So Area of Rectangle 1 = l x b

                       = 7 x 2

                       = 14cm²

So Area of Rectangle 2 = l x b

                       = 7 x 4

                       = 28cm²

Total Area = 14cm² + 28cm²

           = 42cm²

^{Watch the video below to get more familiar with finding perimeter and Area of compound figures.}

^{https://www.tiktok.com/@fathimath_azlifa/video/7361734854398053633?_t=8loyHMGMVqi&_r=1}

^{If you are confident in this lesson, try the worksheet on the link below to see how confident you are:}

^{https://drive.google.com/file/d/1EnXG__9fagyNluYOWBUozi03tc9CeJdo/view?usp=sharing}

Perimeter VS Area (Other shapes)

The formulas used to find the perimeter and Area of different shapes are given below.

PERIMETER	AREA
RECTANGLE = 2 (Length + Breadth) = 2 (l + b)	RECTANGLE = Length x Breadth = l x b
SQUARE = 4 (Length) = 4l	SQUARE = Length x Length = l x l
TRIANGLE = Sum of all sides	TRIANGLE = ½ (Base x Height) = ½ bh
PARALLELOGRAM = Sum of all sides	PARALLELOGRAM = Base x Height = B x H
CIRCLE = 2 x π x radius = 2πr (OR) = π x diameter = πd	CIRCLE = π x radius x radius = πr2
TRAPEZIUM = Sum of all sides	TRAPEZIUM = ½ (a + b) x height a + b is the sum of all parallel sides TRAPEZIUM = ½ (a + b) h

 

To see how familiar you are with the basics of perimeter and Area and their formula, play this game.

If you want to practice with some simple shapes, try the worksheet below:

https://drive.google.com/file/d/1hlK6z8_sJswqu0s7PilOjvax5tyGshyU/view?usp=sharing

 

 

Perimeter & Area (Introduction)

Imagine you are given a piece of a picnic cloth and the teacher is asking you how much ribbon needs to be used to decorate around the cloth. It is a group task with each group getting a cloth that are either rectangular or squared and the teacher is only going to provide as much ribbon as you ask for. So, how can you tell the exact measure of ribbon needed? 

Now as you learned in early grades, this is pretty simple. You find the PERIMETER of the cloth.

What is Perimeter?

The word comes from two Greek words; peri, meaning 'around', and metron, meaning 'measure'. So perimeter is the distance or measure around something. Unit is cm, m, km as measured in length.

Calculating Perimeter

Now let's take the image of a rectangular cloth below as an example for one of the picnic cloths given by the teacher.

When we take the distance around the cloth, it will be somewhat like the image on the right, which is why the formula for Perimeter of rectangle is:

P = 2 (length + breadth/width)

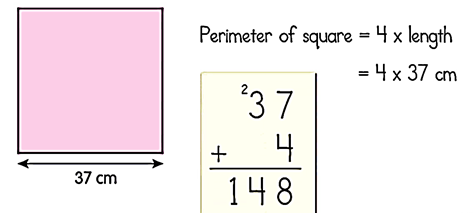
The groups which received the square cloth like the one below, will use the formula below to find how much ribbon they need:

P = 4 x length

       
                                           

Now let's say the square has a length of 37m on each side. By applying the formula the total perimeter of the square would be 148cm, which is how much ribbon they need for decoration.

So, if the teacher asks to find the group which needed the most ribbon, we can just compare the perimeters and find out the answer.

Moving on with the lesson, the teacher wanted to find out which group received the biggest cloth. Now, how do we find that?

As you may already be familiar, to find the biggest cloth we need to know the surface taken up by each cloth, which is also known as the AREA of a shape.

What is Area?

The word 'Area' means a vacant piece of ground in Latin. In Mathematics, it is defined as the total space occupied by a flat 2D shape of an object. It is the number of unit squares occupied by the surface of a closed figure, which is why is is measured in square units. (cm², m², km²)

Calculating Area

The figure on the left shows why Area is measured in square units. Area shows how many unit squares are needed to cover an object. Thus, the Area of rectangle is given by the formula:

A = length x breadth

While the Area of square is given by the formula:

A = length x length

Which means the rectangular image on the right has an Area of 12cm²

(Area = length x breadth, Area = 4 x 3, which is 12cm² )

It's time to see the real life applications of perimeter and Area.

Watch the presentation below to see real life applications of perimeter and area:

https://docs.google.com/presentation/d/1ickcccFKM0ul4bYpeL6I1K7PJE0Padi3/edit?usp=sharing&ouid=105238515076765631615&rtpof=true&sd=true